Let x(t) be a continuous-time complex exponential signal,

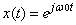
with fundamental frequency w₀ and fundamental period

Consider the discrete-time signal obtained by taking equally spaced samples of x(t) - that is

 (a) Show that x[n] is periodic if and only if  T / T₀ is a rational number - that is, if and only if some multiple of  the
       sampling interval exactly equals a multiple of the period of x(t) .

 (b) Suppose that x [n] is periodic - that is, that

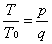
        where p and q are integers. What are the fundamental period and fundamental frequency as a fraction of
        w₀T .

 (c) Again assuming that  T / T₀ satisfies the above equation, determine precisely how many periods of x(t) are
       needed to obtain the samples that form a single period of  x[n] .